你能用偏微分方程模拟红旗在空中飘的运动模式吗?
我们公司在面试数学背景比较强的应试者时都会问这样一个经典的问题。
绝大部分应试者在面对这个问题的时候都是一脸懵逼的状态,宛如当年笔者在研究生面试时被导师问到这个问题一样惊讶。偏微分方程还可以这样玩?
今天就给大家分析一下为什么见知数据,一家做企业级现金流数据分析的公司会有这么一道奇怪的题目。我们究竟是想考察应聘者哪方面的能力?
红旗随风摆动是我们生活中常见的事情,一个2岁的孩童可能会看着红旗变换形状而随之挥舞彩带,看着它咯咯的笑。
正因为它如此的普通,以至于很少有人会思考这个运动的细节究竟是怎样的,就如同万有引力一直存在,而在牛顿之前却没有人可以量化的描述它。
那么什么是偏微分方程呢?红旗的摆动又如何用偏微分方程来描述呢?
这里举一个大家都知道的例子,自由落体运动的位移公式:
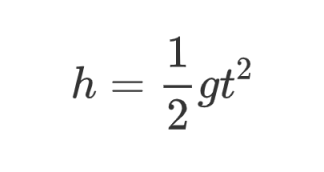
这里的g就是重力加速度,也就是速度的微分。所以,其实上述公式就是用一个常微分方程来描述小球下落的运动。
对于旗面的运动,其实它每一个时刻的整体形状都是由旗面的每一个点的每一个位置组成的。这些点是连续的,且影响这些点位置的因素有多个,比如力和时间。因此要描述这样的状态就要用到偏微分方程。
当然笔者也明白,用这样的问题去考数学系的学生可能有失偏颇。虽然说知识点都有教过,但能把知识点运用到生活中的还是很少,毕竟应付各种古怪的理论证明题就够学生头大了。相反这个问题如果是给物理系的学生,也许因为许多常用方程比如波动方程、热传导方程都是偏微分方程,直觉上更熟悉,反而会有一些思路。
当然,我们问这个问题并不是真的希望谁把方程写出来,而是想看解题思路。一个看似平常的现象,真要分析起来就需要用到许多知识,比如极限的思想。
描述红旗的表面的确很复杂。但是面是由线组成的,是否可以先描述线的运动呢?
如果线也太复杂,那么线又是由点组成的,能否再退一步,描述点的运动呢?
分析到点的运动的层面,其实很多人高中时期就学过了受力分析的相关知识。我们可以通过N个点来模拟红旗的一个面,假设每个点只和最近的几个点发生力的作用,再设定一个初始状态初始的力,可能就能模拟后续的连续运动了。
再或者,我可不可能在不推导计算的前提下写出这个公式呢?我应该去哪里找呢?
如果玩过电子游戏,就能联想到游戏里有很多旗子飘动的场景。而游戏中的场景都是电脑通过模拟计算出来的,那么它必然有一个公式,如同游戏中的影子就是设定一个光源再,通过光是直线传播的公式来计算出影子的位置与大小。
所以找一些游戏开发工具中的物理引擎源码,可能就能找到类似的公式了。

见知数据做企业级现金流分析,其实和分析红旗飘动的运动模式很像。
乍一听都觉得很简单:现金流嘛,不就是流水账?不就是收入、支出、余额?似乎每个财务人员都能理的清楚。
但是如果往细了想,你如何通过已知现金流数据来描述企业目前的状态?是否有个公式能预测出它未来的变化?运营良好的企业的现金流究竟有什么内在共性?为什么同样一家连锁品牌店规模相似,一家赚钱另一家亏本?
这些都像红旗飘动一样,是连续的相互影响的各个因子的综合作用产生的结果。如果不具备把复杂问题一步步拆解到点从而解决问题的能力,当我们遇到企业资金和内外部环境变化错综复杂的情况,就只能用一句“市场无法预测”来回避。那么还如何为客户提供高效有用的现金流分析服务?如何称得上一款智能的现金流分析系统呢?
见知数据的未来,不仅要为企业客户和机构分析资金,我们还希望从更高的层面去探寻企业现金流的隐含逻辑,实现我们的初心:见微知著。
或许哪一天我们会发现企业级现金流领域的质能方程,相信泡利不相容原理就会诞生在这里!





